Answered 4 years ago Author has 347K answers and 234M answer views For finding the ratios of a triangle whose angles are 30, 60 and 90 degrees use the sine formula a/sin 90 = b/sin 30 = c/sin 60, or a/1 = b/05 = c/0866 = k, or if k = 1 unit, then a = 1 unit, b 2 units and c= 0866 unitsWe know from Plane (Euclidean) Geometry that in a right triangle, the length of the side opposite the 30 degree angle is equal to onehalf the length of the hypotenuse About Triangle A triangle is a unique right triangle whose angles are 30º, 60º, and 90º The triangle is unique because its side sizes are always in the proportion of 1 √ 32 Any triangle of the kind can be fixed without applying longstep approaches such as the Pythagorean Theorem and trigonometric features

The Complete Guide To The 30 60 90 Triangle
Ratio of sides in a 30 60 90 triangle
Ratio of sides in a 30 60 90 triangle-Correct answer Explanation We know that in a 3060=90 triangle, the smallest side corresponds to the side opposite the 30 degree angle Additionally, we know that the hypotenuse is 2 times the value of the smallest side, so in this case, that is 10 The formula forA triangle is a special right triangle that contains internal angles of 30, 60, and 90 degrees Once we identify a triangle to be a 30 60 90 triangle, the values of all angles and sides can be quickly identified Imagine cutting an equilateral triangle vertically, right down the middle Each half has now become a 30 60 90 triangle




30 60 90 Right Triangle Side Ratios Expii
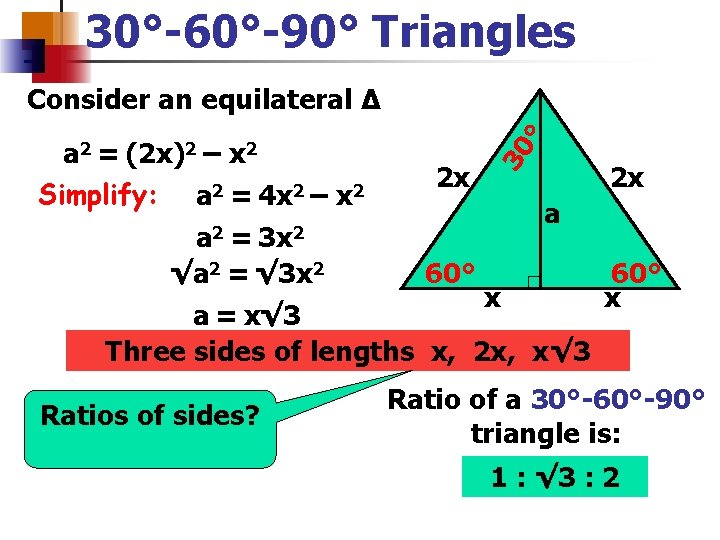
The sides of a right triangle lie in the ratio 1√32 The side lengths and angle measurements of a right triangle Credit Public Domain We can see why these relations should hold by plugging in the above values into the Pythagorean theorem a2 b2 = c2 a2 ( a √3) 2 = (2 a) 2 a2 3 a2 = 4 a2A 30 60 90 triangle completes an arithmetic progression 3030=6030 =90 An arithmetic progression is a sequence of numbers in which the difference of any two successive numbers is a constant For instance, 2,4,6,8 is an arithmetic progression with a constant of 2In the study of trigonometry the 30 60 90 triangle is considered a special triangle knowing the ratio of the sides of a 30 60 90 triangle allows us to find the exact values of the three trigonometric functions sine cosine and tangent for the angles 30
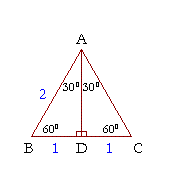
Here is the proof that in a 30°60°90° triangle the sides are in the ratio 1 2 It is based on the fact that a 30°60°90° triangle is half of an equilateral triangle Draw the equilateral triangle ABC Then each of its equal angles is 60° (Theorems 3 and 9) Draw the straight line AD bisecting the angle at A into two 30° anglesHow would one find the other two sides of a rightangled triangle having angles 30°, 60°, and 90° if the hypotenuse of the triangle is 2m? A is a scalene triangle and each side has a different measure Since it's a right triangle, the sides touching the right angle are called the legs of the triangle, it has a long leg and a short leg, and the hypotenuse is the side across from the right angle
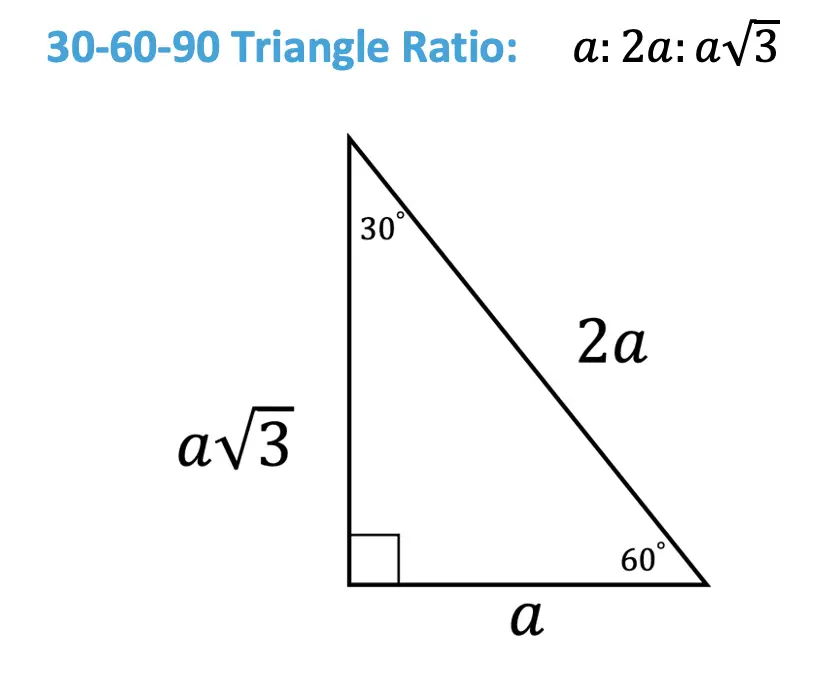
As one angle is 90, so this triangle is always a right triangle As explained above that it is a special triangle so it has special values of lengths and angles The basic triangle sides ratio is The side opposite the 30° angle x The side opposite the 60° angle x * √3 The side opposite the 90° angle 2x A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides are also always in the same ratio to each other The side opposite the 30º angle is the shortest and the length of it is usually labeled as x The side opposite the 60º angle has aA right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1√3 2




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com




Velocity
A triangle is a special right triangle whose angles are 30º, 60º, and 90º The triangle is special because its side lengths are always in the ratio of 1 √32 Any triangle of the form can be solved without applying longstep methods such as the Pythagorean Theorem and trigonometric functions The 30 60 90 triangle is special because it forms an equilateral triangle when a mirror image of itself is drawn, meaning all sides are equal!Proving the ratios between the sides of a triangleWatch the next lesson https//wwwkhanacademyorg/math/geometry/right_triangles_topic/special_rig




Special Right Triangles Part 1 45 45 90 And 30 60 90 Youtube




30 60 90 Triangles
How are they different?Given that the leg opposite the 30° angle for a triangle has a length of 12, find the length of the other leg and the hypotenuse The hypotenuse is 2 × 12 =A right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1 √3 3 2 That is to say, the hypotenuse is twice as long as the shorter leg, and




30 60 90 Triangle Side Ratios Proof Youtube



Solution In A Triangle Abc Angle A 30 Angle B 90 And Ab Is 12 Cm Find The Length Of
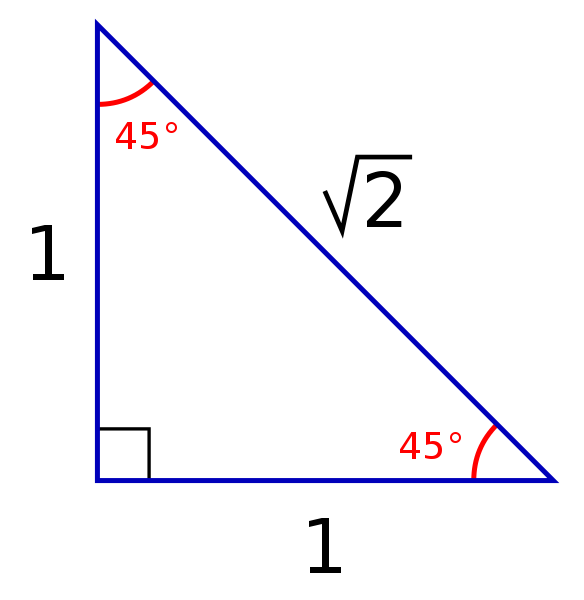
The triangle is called a special right triangle as the angles of this triangle are in 45 45 90 triangle calculator is a dedicated tool to solve this special right triangle Find out what are the sides, hypotenuse, area and perimeter of your shape and learn about 45 45 90 triangle formula, ratio and rules If you want to know more about another popular right triangles, check out this 30 60 90 triangle tool and the calculator forProve Side Ratios for Triangle = 1sqrt (3)2




A Quick Guide To The 30 60 90 Degree Triangle Dummies




The Side Lengths Of A 30 60 90 Triangle Are In The Ratio 1 3 2 What Is Sin 30 Brainly Com
The triangle is a special right triangle, as it has a special relationship between its sides If we know the measure of at least one side of the triangle, the special proportions of sides of the triangle could be used to determine the measure of other sides of the same triangle30°60°90° Triangles There is a special relationship among the measures of the sides of a 30 ° − 60 ° − 90 ° triangle A 30 ° − 60 ° − 90 ° triangle is commonly encountered right triangle whose sides are in the proportion 1 3 2 The measures of the sides are x, x 3, and 2 xSee also Side /angle relationships of a triangle In the figure above, as you drag the vertices of the triangle to resize it, the angles remain fixed and the sides remain in this ratio Corollary If any triangle has its sides in the ratio 1 2 √3, then it is a triangle




30 60 90 Right Triangle Side Ratios Expii




Special Right Triangles 30 60 90 Ck 12 Foundation
The other one is the 45 45 90 triangle These triangles are special triangles because the ratio of their sides are known to us so we can make use of this information to help us in right triangle trigonometry problems In the case of the triangle, their side's ratios are 1The triangle is one example of a special right triangle It is right triangle whose angles are 30°, 60° and 90° The lengths of the sides of a triangle are in the ratio of 1√32 The following diagram shows a triangle and the ratio of the sides Scroll down the page for more examples and solutions on how to use30 60 90 and 45 45 90 Triangle Calculator I N S T R U C T I O N S Start by entering the length of a triangle side Then click on which type of side it is The 5 choices you have are As soon as you click that box, the output boxes will automatically get filled in by the calculator Clicking "RESET" clears all of the boxes




30 60 90 Triangle Definition Theorem Formula Examples
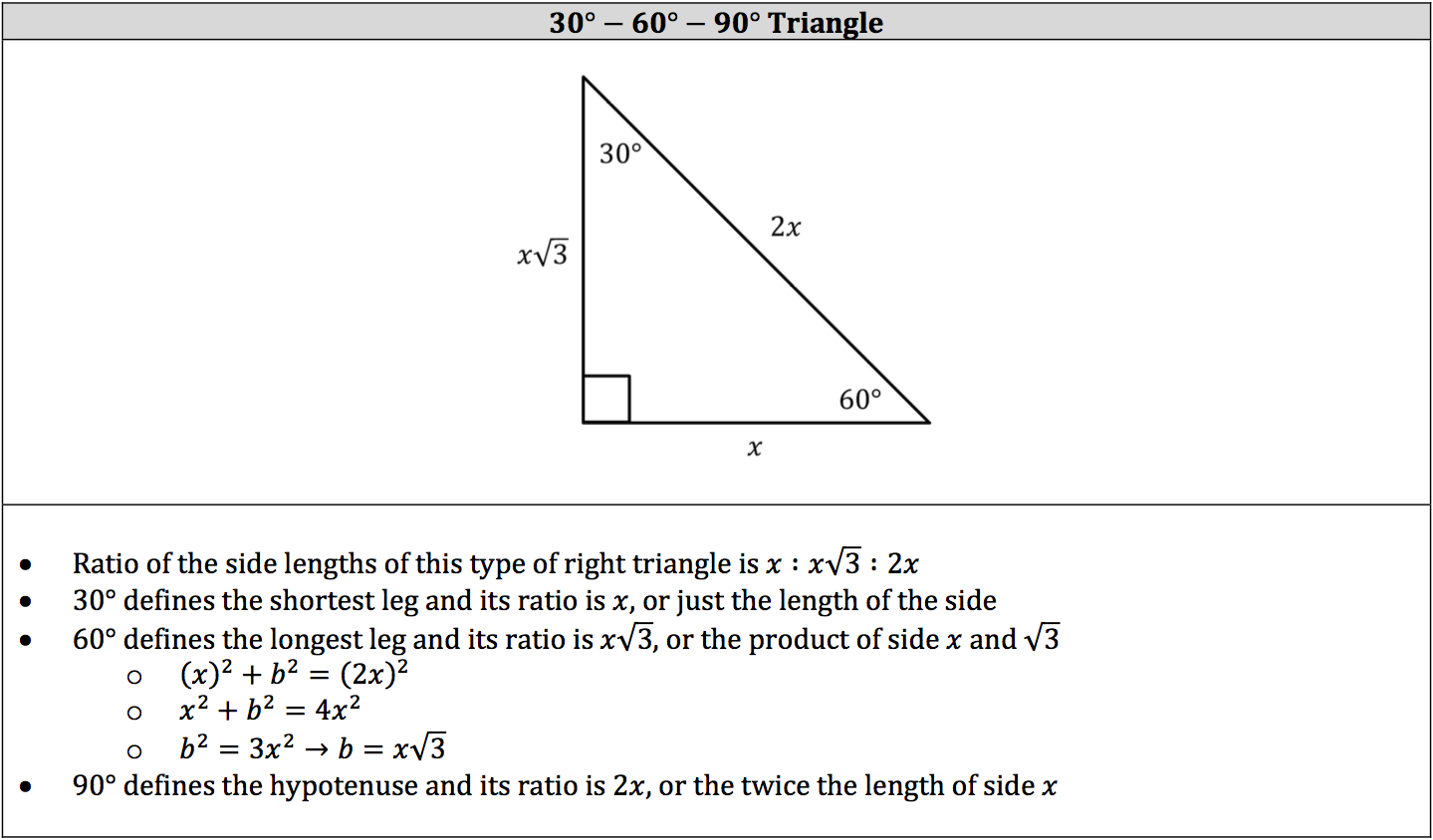



30 60 90 Triangle Piqosity Adaptive Learning Student Management App
Qualities of a Triangle A triangle is special because of the relationship of its sides Hopefully, you remember that the In a triangle, how many sides do you need to know in order to determine the remaining sides?The lengths of the sides of a 30°60°90° triangle are in the ratio of 1 √3 2 You can also recognize a 30°60°90° triangle by the angles As long as you know that one of the angles in the rightangle triangle is either 30° or 60° then it must be a 30°60°90° special right triangle A right triangle with a 30° angle or 60




30 60 90 Triangle Theorem Ratio Formula Video




Learn About The 30 60 90 Triangle Caddell Prep Online
The triangle ratio for the length of the sides is as follows The hypotenuse is twice the shorter leg The longer leg is {eq}\sqrt{3} {/eq} times the shorter sideA special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist Angle based right triangle , (Angles that form a simple ratio) Side based right triangle 345 (The lengths of the sides form a whole number ratio), approx angles 3753The property is that the lengths of the sides of a triangle are in the ratio 12√3 Thus if you know that the side opposite the 60 degree angle measures 5 inches then then this is √3 times as long as the side opposite the 30 degree so the side opposite the 30 degree angle is 5




30 60 90 Triangles Hd Youtube
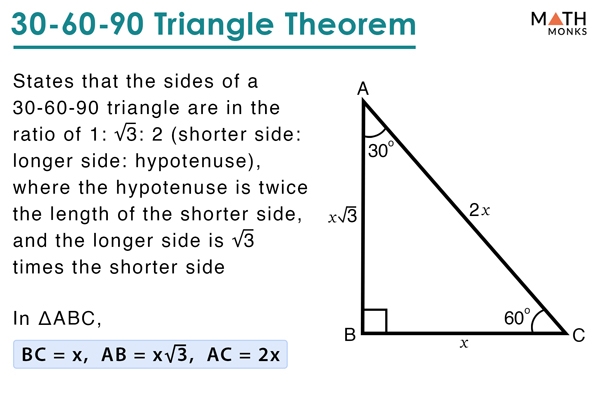



30 60 90 Triangle Definition Formulas Examples
How are the proofs for the side length ratios of and triangles similar? View CamScanner__1758_134jpg from MATHEMATIC 104 at University of Nairobi The ratio of the sides is then abc = 12 V52A triangle is one of the few special right triangles with angles and side ratios that are consistent and predictable Specifically, every triangle has a 30º angle, a 60º angle, and a 90º angle Since these angles stay the same, the ratio between the
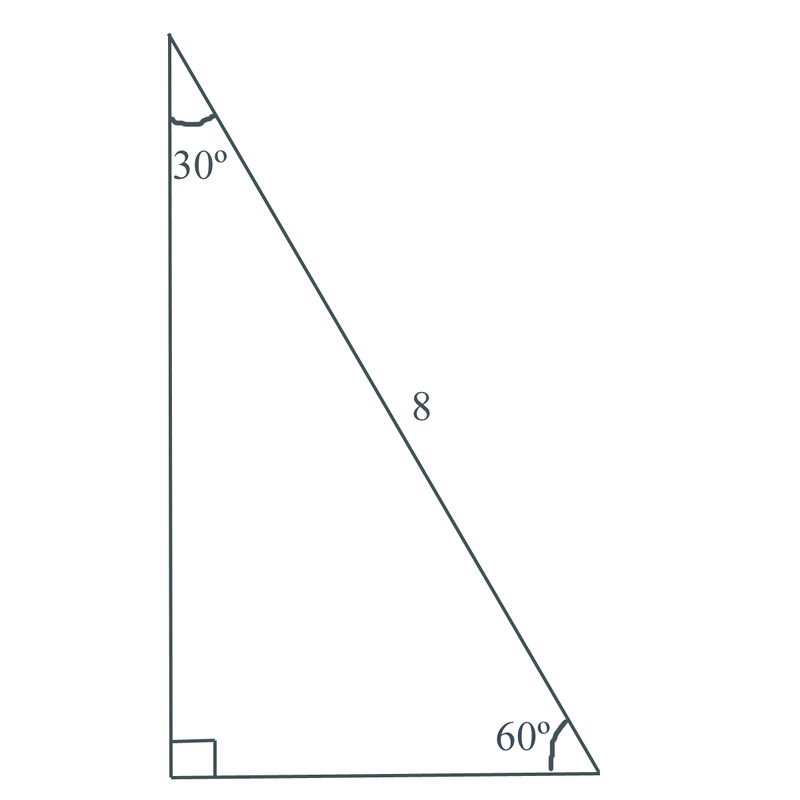



Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation
Since the right angle is always the largest angle, the hypotenuse is always the longest side using property 2 We can use the Pythagorean theorem to show that the ratio of sides work with the basic triangle above a2b2=c2 12(3–√)2=13=4=c2 4–√=2=cThis allows us to find the ratio between each side of the triangle by using the Pythagorean theoremA right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1sqrt (3)2 That is to say, the hypotenuse is twice as long as the shorter leg, and




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com




The Complete Guide To The 30 60 90 Triangle
Special Triangles Isosceles and Calculator This calculator performs either of 2 items 1) If you are given a right triangle, the calculator will determine the missing 2 sides Enter the side that is known After this, press Solve Triangle 2) In addition, the calculator will allow you to same as Step 1 with a right triangleWhat I want to do in this video is discuss a special class of triangles called triangles and I think you know why they're called this the measures of its angles are 30 degrees 60 degrees and 90 degrees and what we're going to prove in this video this tends to be a very useful result at least for a lot of what you see in a geometry class and then later on in trigonometry class is the ratios A triangle is a special right triangle whose angles are 30º, 60º, and 90º The triangle is special because its side lengths are always in the ratio of 1 √32
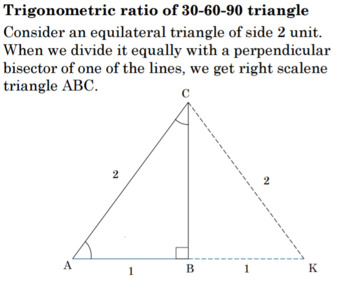



Trigonometry Of 30 60 90 Right Triangle 1 Lesson Plan G Srt C 6 Tpt



The Easy Guide To The 30 60 90 Triangle
It is based on bisecting an equilateral triangle and using the Pythagorean theorem A 30°60°90° triangle is formed when an equilateral triangle is bisected This makes the Hypotenuse a length of x, and the short side a length of (1/2)xThis is a triangle whose three angles are in the ratio 1 2 3 and respectively measure 30° (π / 6), 60° (π / 3), and 90° (π / 2)The sides are in the ratio 1 √ 3 2 The proof of this fact is clear using trigonometryThe geometric proof is Draw an equilateral triangle ABC with side length 2 and with point D as the midpoint of segment BC



The Easy Guide To The 30 60 90 Triangle



What Are The Side Ratios For A 30 60 90 Triangle Quora



30 60 90 Special Triangles Geometry Mathsux 2



30 60 90 Right Triangle Side Ratios Expii




Special Right Triangles 30 60 90 Triangle Side Ratios Proof Pbs Learningmedia



30 60 90 Triangle Formulas Rules And Sides Science Trends




30 60 90 Triangle Calculator Formula Rules



We Make A Living By What We Get




30 60 90 Triangle



How Come In My Geometry Class I Was Taught Special Triangles 30 60 90 Triangles Had The Sides 1 1 2 3 2 But In My Trigonometry Class I Was Taught That The Sides For



The Easy Guide To The 30 60 90 Triangle



What Is The Ratio Of Sides Of A Triangle If The Angles Are 30 60 90 Quora
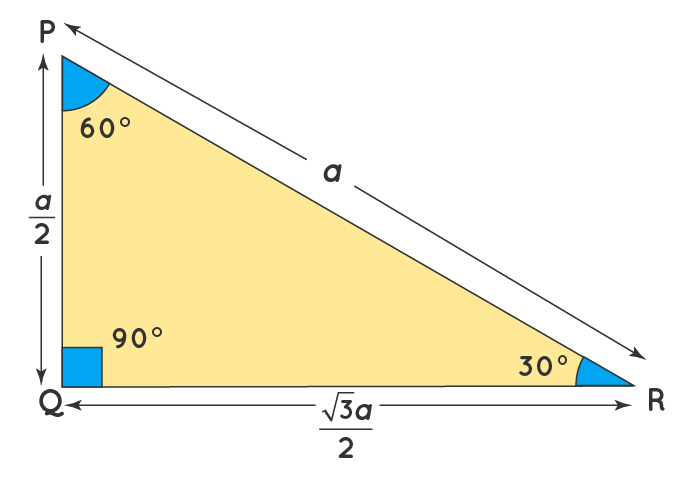



30 60 90 Triangle Definition Theorem Formula Examples




4 43 30 60 90 Right Triangles K12 Libretexts



Tarantamath Licensed For Non Commercial Use Only Razan 10 3



Special Right Triangles Definition And Use The Triangle Definition There Are Many Right Angle Triangles Today We Are Most Interested In Right Ppt Download




How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies




Special Right Triangles




How To Use The Special Right Triangle 30 60 90 Studypug



Special Right Triangles Activity Builder By Desmos




30 60 90 Triangle Theorem Ratio Formula Video




The Side Lengths Of A 30 60 90 Triangle Are In The Ratio 1 3 2 What Is Sin 30 Brainly Com




The Secondary Classroom Can Be Fun Too Discovering Special Right Triangles




Special Right Triangles Review Article Khan Academy




Solved Deriving The Ratio Of The Sides Of A 30 60 90 Chegg Com




Instructions Use The Ratio Of A 30 60 90 Triangle To Solve For The Variables Leave Your Answers As Brainly Com
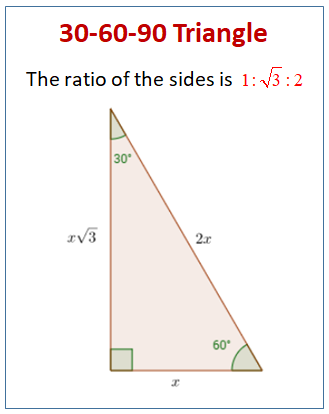



30 60 90 Special Right Triangles Videos Worksheets Examples Solutions
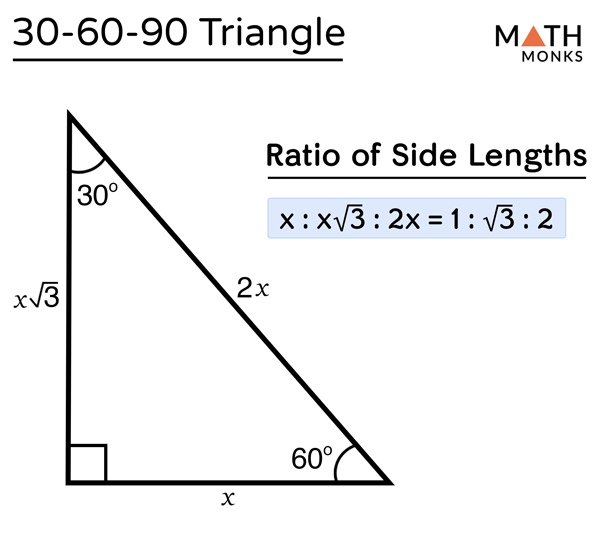



30 60 90 Triangle Definition Formulas Examples



1
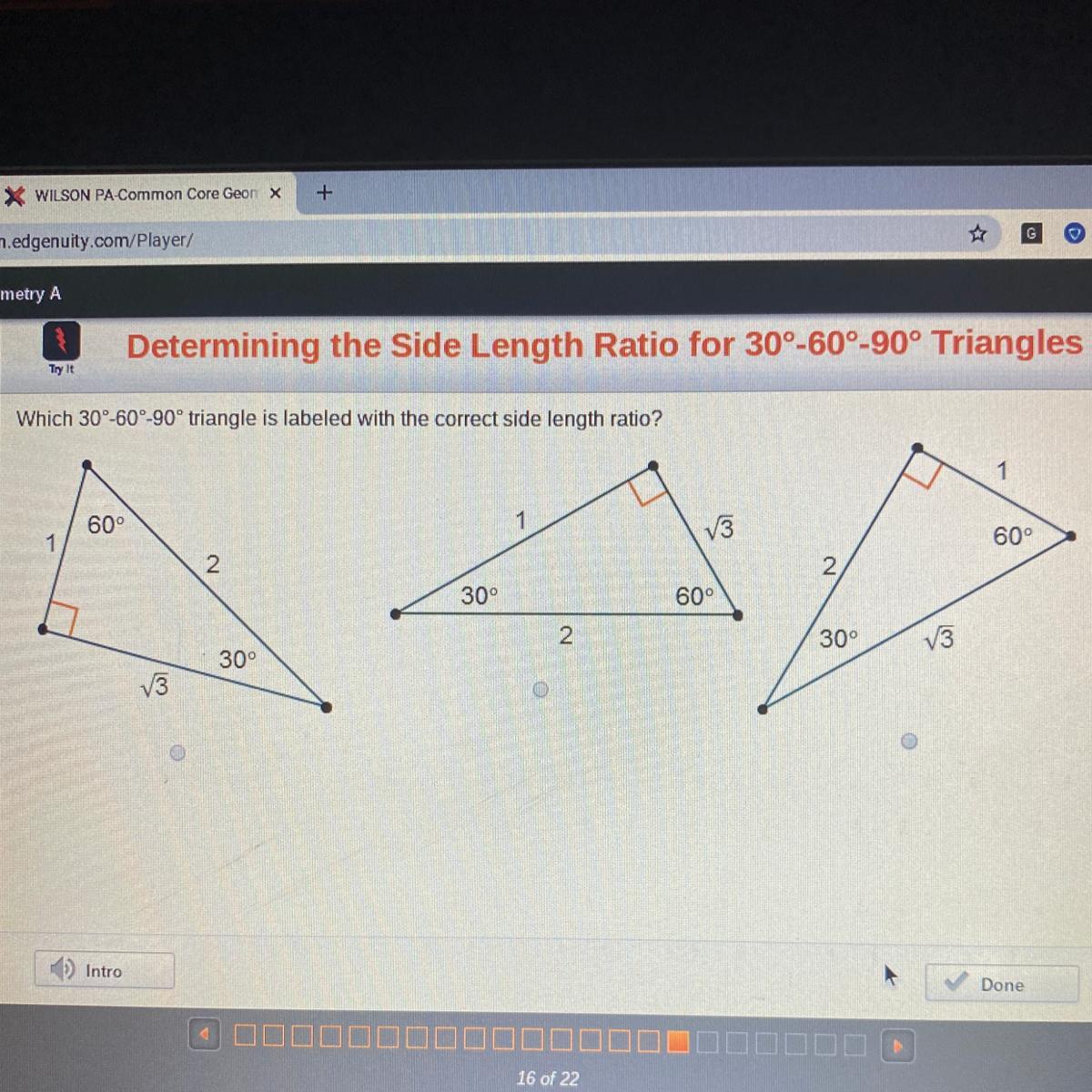



Which 30 60 90 Degree Triangle Is Labeled With The Correct Side Length Ratio




30 60 90 Triangle Theorem Ratio Formula Video
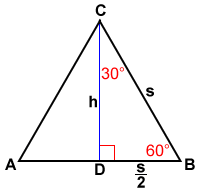



30 60 90 Triangle
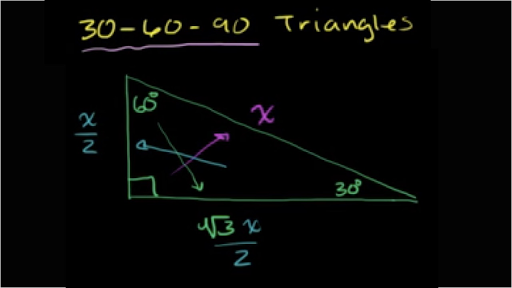



Special Right Triangles Proof Part 1 Video Khan Academy




Special Right Triangles Part 3 30 60 90 Youtube
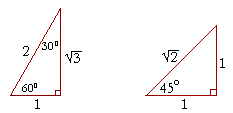



The 30 60 90 Triangle Topics In Trigonometry



1




Special Right Triangles Fully Explained W 19 Examples




30 60 90 Right Triangles Solutions Examples Videos




Hints For Problem 5 To Find The Height Of An Chegg Com




Special Right Triangles Definition And Use The Triangle Definition There Are Many Right Angle Triangles Today We Are Most Interested In Right Ppt Download



1




30 60 90 Triangle Theorem Ratio Formula Video



30 60 90 Triangle Rules




30 60 90 Triangle Explanation Examples




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation
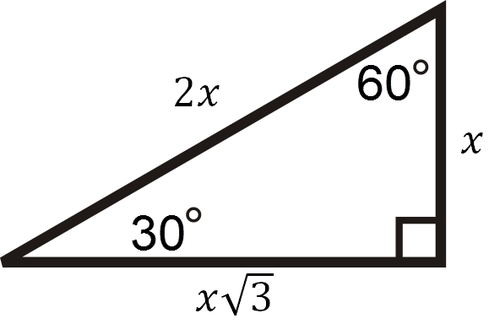



Special Right Triangles And Ratios Geometry




Which 30 60 90 Degree Triangle Is Labeled With The Correct Side Length Ratio Brainly Com




30 60 90 Triangle Definition Theorem Formula Examples




File 30 60 90 Triangle Svg Wikimedia Commons




30 60 90 Triangle Side Ratios Proof Right Triangles And Trigonometry Geometry Khan Academy Youtube



What Is The Ratio Of Sides Of A Triangle If The Angles Are 30 60 90 Quora




30 60 90 Triangle Theorem Ratio Formula Video




The Complete Guide To The 30 60 90 Triangle



1
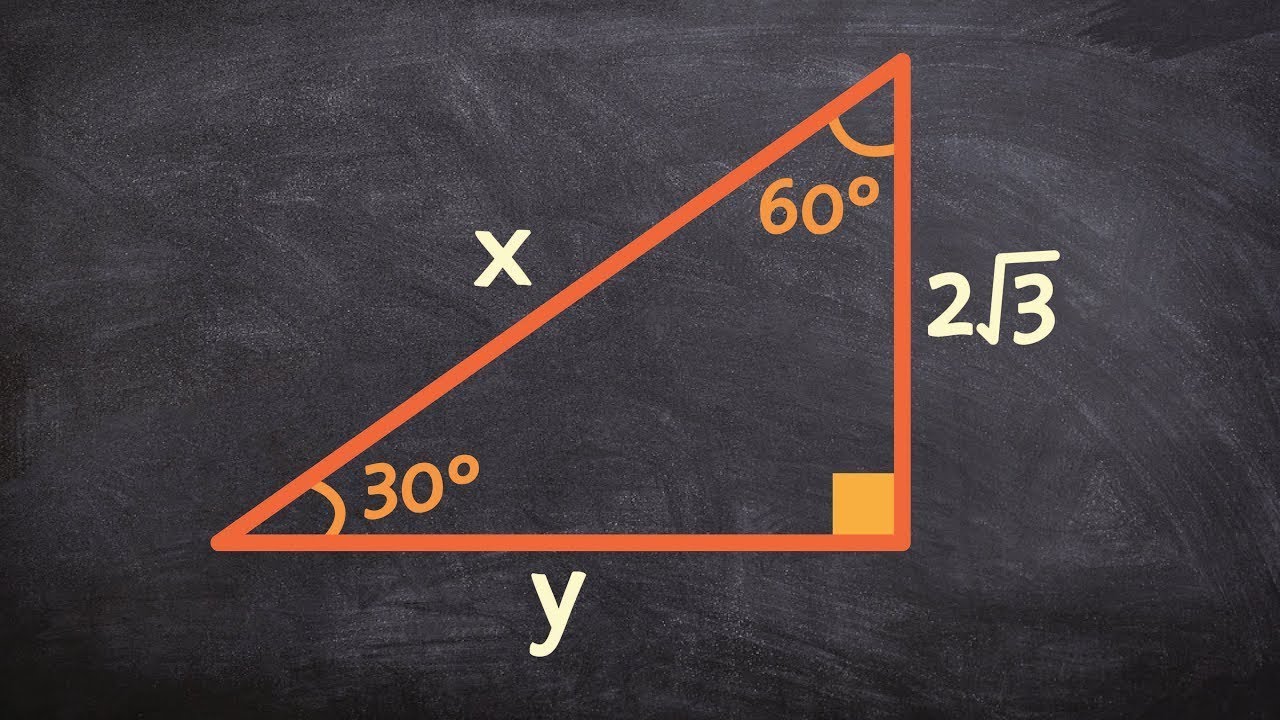



Find The Missing Sides Of A Triangle Given A 30 60 90 Triangle Youtube



Right Triangles With Special Angles And Side Ratios



The Easy Guide To The 30 60 90 Triangle



The Easy Guide To The 30 60 90 Triangle
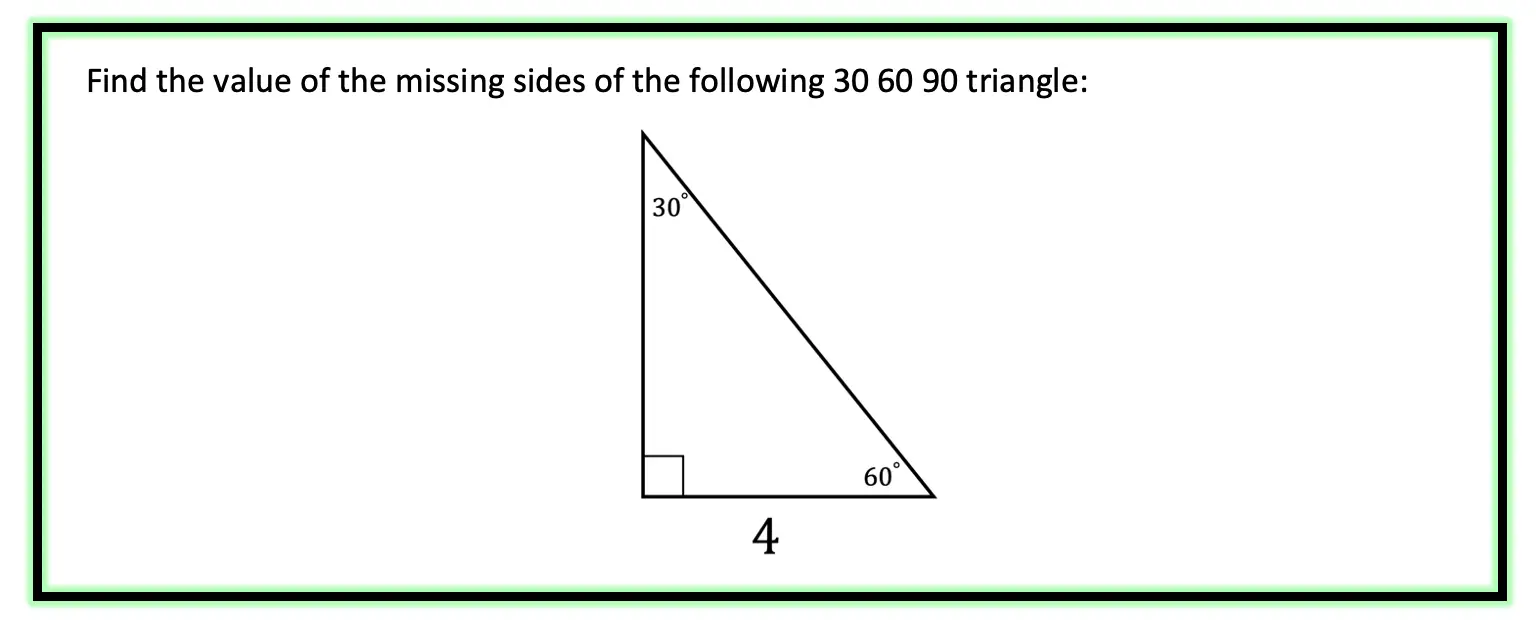



30 60 90 Special Triangles Geometry Mathsux 2
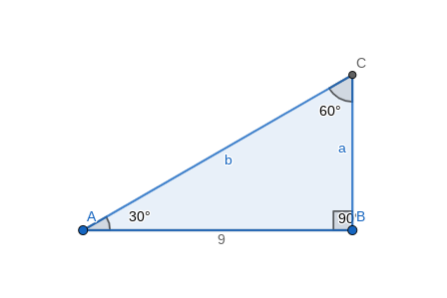



Activity 22 Construct A 30 60 90 Triangle Geogebra




How To Work With 30 60 90 Degree Triangles Education Is Around



A 30 60 90 Triangle Math Central



A 30 60 90 Triangle



Find The Value Of The Sine Or Cosine Functions Of An Angle Given A Point On Its Terminal Side Precalculus




The 30 60 90 Triangle Topics In Trigonometry




Pythagorean Theorem Review 5 Questions If A Triangle




How To Find The Area Of A Regular Polygon Using Special Right Triangles Geometry Study Com




Solved Question 6 What Is The Ratio Of The Side Lengths Of A Chegg Com




Special Right Triangles Review Article Khan Academy




A Quick Guide To The 30 60 90 Degree Triangle Dummies




30 60 90 Triangle Explanation Examples




The 30 60 90 Triangle Topics In Trigonometry




30 60 90 Triangles Spock S Guide To Math 4




30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Calculator Formula Rules




30 60 90 Right Triangle Side Ratios Expii




30 60 90 Triangle Theorem Ratio Formula Video
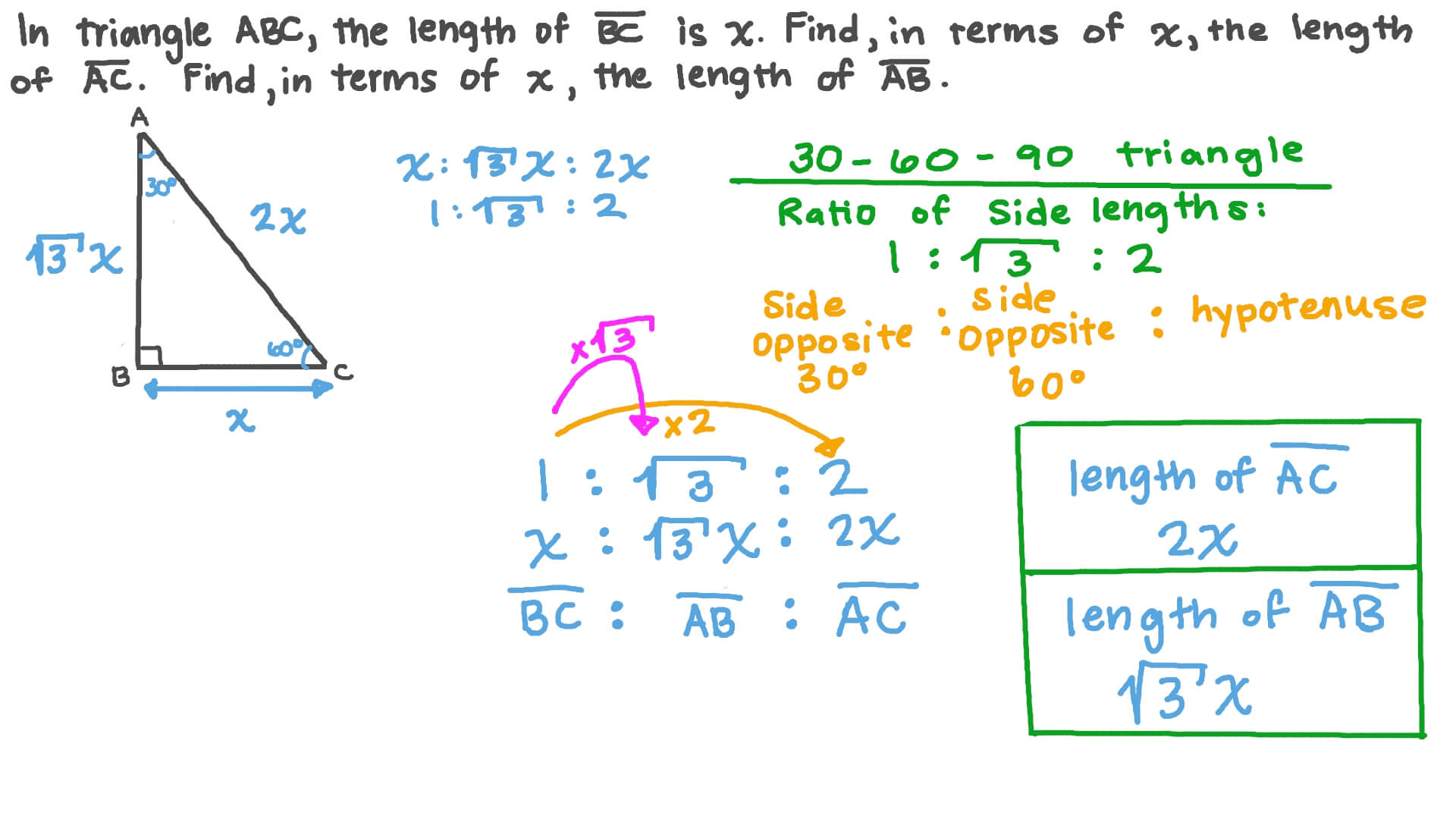



Question Video The Side Lengths Of 30 60 90 Triangles Nagwa




Special Right Triangles 30 60 90 And The 45 45 90 Graphic Organizer Worksheet




30 60 90 Triangle Explanation Examples




30 60 90 Triangle Definition Math Open Reference



5 5 Special Triangles



0 件のコメント:
コメントを投稿